Find a General Solution to the Following Trigonometric Equation
6.1: Solving Trigonometric Equations
-
- Last updated
- Save as PDF
- Page ID
- 3342
An equation involving trigonometric functions is called a trigonometric equation. For example, an equation like
\[\nonumber
\tan\;A ~=~ 0.75 ~,
\]
which we encountered in Chapter 1, is a trigonometric equation. In Chapter 1 we were concerned only with finding a single solution (say, between \(0^\circ \) and \(90^\circ\)). In this section we will be concerned with finding the most general solution to such equations.
To see what that means, take the above equation \(\tan\;A = 0.75 \). Using the \(\fbox{\(\tan^{-1}\)}\) calculator button in degree mode, we get \(A=36.87^\circ \). However, we know that the tangent function has period \(\pi \) rad \(= 180^\circ \), i.e. it repeats every \(180^\circ \). Thus, there are many other possible answers for the value of \(A \), namely \(36.87^\circ + 180^\circ \), \(36.87^\circ - 180^\circ \), \(36.87^\circ + 360^\circ \), \(36.87^\circ - 360^\circ \), \(36.87^\circ + 540^\circ \), etc. We can write this in a more compact form:
\[\nonumber
A ~=~ 36.87^\circ \;+\; 180^\circ k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
This is the most general solution to the equation. Often the part that says "for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)'' is omitted since it is usually understood that \(k \) varies over all integers. The general solution in radians would be:
\[\nonumber
A ~=~ 0.6435 \;+\; \pi k \quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.1
Solve the equation \(\;2\,\sin\;\theta \;+\;1 ~=~ 0 \).
Solution:
Isolating \(\sin\;\theta \) gives \(\;\sin\;\theta ~=~ -\tfrac{1}{2} \). Using the \(\fbox{\(\sin^{-1}\)}\) calculator button in degree mode gives us \(\theta = -30^\circ \), which is in QIV. Recall that the reflection of this angle around the \(y\)-axis into QIII also has the same sine. That is, \(\sin\;210^\circ = -\tfrac{1}{2} \). Thus, since the sine function has period \(2\pi \) rad \(= 360^\circ \), and since \(-30^\circ \) does not differ from \(210^\circ \) by an integer multiple of \(360^\circ \), the general solution is:
\[\nonumber
\boxed{\theta ~=~ -30^\circ \;+\; 360^\circ k \quad\text{and}\quad 210^\circ \;+\;
360^\circ k} \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
In radians, the solution is:
\[\nonumber
\boxed{\theta ~=~ -\dfrac{\pi}{6} \;+\; 2\pi k \quad\text{and}\quad \dfrac{7\pi}{6} + 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
For the rest of this section we will write our solutions in radians.
Example 6.2
Solve the equation \(\;2\cos^2 \;\theta \;-\; 1 ~=~ 0 \).
Solution:
Isolating \(\;\cos^2 \;\theta \) gives us
\[\nonumber
\cos^2 \;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \pm\,\frac{1}{\sqrt{2}}
\quad\Rightarrow\quad \theta ~=~ \frac{\pi}{4}\;,~\frac{3\pi}{4}\;,~\frac{5\pi}{4}\;,~
\frac{7\pi}{4}~,
\]
and since the period of cosine is \(2\pi \), we would add \(2\pi k \) to each of those angles to get the general solution. But notice that the above angles differ by multiples of \(\frac{\pi}{2} \). So since every multiple of \(2\pi \) is also a multiple of \(\frac{\pi}{2} \), we can combine those four separate answers into one:
\[\nonumber
\boxed{\theta ~=~ \frac{\pi}{4} \;+\; \frac{\pi}{2}\,k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.3
Solve the equation \(\;2\,\sec\;\theta ~=~ 1 \).
Solution:
Isolating \(\;\sec\;\theta \) gives us
\[\nonumber
\sec\;\theta ~=~ \frac{1}{2} \quad\Rightarrow\quad \cos\;\theta ~=~ \frac{1}{\sec\;\theta} ~=~ 2~,
\]
which is impossible. Thus, there is \(\fbox{no solution}\).
Example 6.4
Solve the equation \(\;\cos\;\theta ~=~ \tan\;\theta \).
Solution:
The idea here is to use identities to put everything in terms of a single trigonometric function:
\[\nonumber \begin{align*}
\cos\;\theta ~&=~ \tan\;\theta\\ \nonumber
\cos\;\theta ~&=~ \frac{\sin\;\theta}{\cos\;\theta}\\ \nonumber
\cos^2 \;\theta ~&=~ \sin\;\theta\\ \nonumber
1 \;-\; \sin^2 \;\theta ~&=~ \sin\;\theta\\ \nonumber
0 ~&=~ \sin^2 \;\theta \;+\; \sin\;\theta \;-\; 1
\end{align*}\]
The last equation looks more complicated than the original equation, but notice that it is actually a quadratic equation: making the substitution \(x=\sin\;\theta \), we have
\[\nonumber
x^2 \;+\; x \;-\; 1 ~=~ 0 \quad\Rightarrow\quad x ~=~ \frac{-1 \;\pm\; \sqrt{1 - (4)\,(-1)}}{
2\,(1)} ~=~ \frac{-1 \;\pm\; \sqrt{5}}{2} ~=~ -1.618\;,~0.618
\]
by the quadratic formula from elementary algebra. But \(-1.618 < -1 \), so it is impossible that \(\;\sin\theta = x = -1.618 \). Thus, we must have \(\;\sin\;\theta = x = 0.618 \). Hence, there are two possible solutions: \(\theta = 0.666 \) rad in QI and its reflection \(\pi - \theta = 2.475\) rad around the \(y\)-axis in QII. Adding multiples of \(2\pi \) to these gives us the general solution:
\[\nonumber
\boxed{\theta ~=~ 0.666 \;+\; 2\pi k \quad\text{and}\quad 2.475 \;+\; 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.5
Solve the equation \(\;\sin\;\theta ~=~ \tan\;\theta \).
Solution:
Trying the same method as in the previous example, we get
\[\nonumber \begin{align*}
\sin\;\theta ~&=~ \tan\;\theta\\ \nonumber
\sin\;\theta ~&=~ \frac{\sin\;\theta}{\cos\;\theta}\\ \nonumber
\sin\;\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~\cos\;\theta \;-\; \sin\;\theta ~&=~ 0\\ \nonumber
\sin\;\theta~(\cos\;\theta \;-\; 1) ~&=~ 0\\ \nonumber
&\Rightarrow\quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ 1\\ \nonumber
&\Rightarrow\quad \theta ~=~ 0\;,~\pi \quad\text{or}\quad \theta ~=~ 0\\ \nonumber
&\Rightarrow\quad \theta ~=~ 0\;,~\pi~,
\end{align*}\]
plus multiples of \(2\pi \). So since the above angles are multiples of \(\pi \), and every multiple of \(2\pi \) is a multiple of \(\pi \), we can combine the two answers into one for the general solution:
\[\nonumber
\boxed{\theta ~=~ \pi k} \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.6
Solve the equation \(\;\cos\;3\theta ~=~ \frac{1}{2} \).
Solution:
The idea here is to solve for \(3\theta \) first, using the most general solution, and then divide that solution by \(3 \). So since \(\;\cos^{-1} \frac{1}{2} = \frac{\pi}{3} \), there are two possible solutions for \(3\theta\): \(3\theta = \frac{\pi}{3} \) in QI and its reflection \(-3\theta = -\frac{\pi}{3} \) around the \(x\)-axis in QIV. Adding multiples of \(2\pi \) to these gives us:
\[\nonumber
3\theta ~=~ \pm\,\frac{\pi}{3} \;+\; 2\pi k \qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
So dividing everything by \(3 \) we get the general solution for \(\theta\):
\[\nonumber
\boxed{\theta ~=~ \pm\,\frac{\pi}{9} \;+\; \frac{2\pi}{3} k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\]
Example 6.7
Solve the equation \(\;\sin\;2\theta ~=~ \sin\;\theta \).
Solution:
Here we use the double-angle formula for sine:
\[\nonumber \begin{align*}
\sin\;2\theta ~&=~ \sin\;\theta\\ \nonumber
2\,\sin\theta~\cos\;\theta ~&=~ \sin\;\theta\\ \nonumber
\sin\;\theta~(2\,\cos\;\theta \;-\; 1) ~&=~ 0\\ \nonumber
&\Rightarrow\quad \sin\;\theta ~=~ 0 \quad\text{or}\quad \cos\;\theta ~=~ \frac{1}{2}\\ \nonumber
&\Rightarrow\quad \theta ~=~ 0\;,~\pi \quad\text{or}\quad \theta ~=~ \pm\,\frac{\pi}{3}\\ \nonumber
&\Rightarrow\quad \boxed{\theta ~=~ \pi k \quad\text{and}\quad \pm\,\frac{\pi}{3} \;+\; 2\pi k}
\qquad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\end{align*}
\]
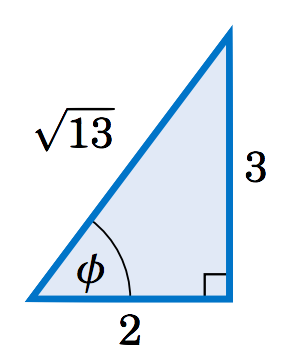
Solution:
We will use the technique which we discussed in Chapter 5 for finding the amplitude of a combination of sine and cosine functions. Take the coefficients \(2 \) and \(3 \) of \(\;\sin\;\theta \) and \(\;-\cos\;\theta \), respectively, in the above equation and make them the legs of a right triangle, as in Figure 6.1.1. Let \(\phi \) be the angle shown in the right triangle. The leg with length \(3 >0 \) means that the angle \(\phi \) is above the \(x\)-axis, and the leg with length \(2>0 \) means that \(\phi \) is to the right of the \(y\)-axis. Hence, \(\phi \) must be in QI. The hypotenuse has length \(\sqrt{13} \) by the Pythagorean Theorem, and hence \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) and \(\;\sin\;\theta = \frac{3}{\sqrt{13}} \). We can use this to transform the equation to solve as follows:
\[\nonumber \begin{align*}
2\,\sin\;\theta \;-\; 3\,\cos\;\theta ~&=~ 1\\ \nonumber
\sqrt{13}\,\left( \tfrac{2}{\sqrt{13}}\,\sin\;\theta \;-\; \tfrac{3}{\sqrt{13}}\,\cos\;\theta
\right) ~&=~ 1\\ \nonumber
\sqrt{13}\,( \cos\;\phi\;\sin\;\theta \;-\; \sin\;\phi\;\cos\;\theta ) ~&=~ 1\\ \nonumber
\sqrt{13}\,\sin\;(\theta - \phi) ~&=~ 1\quad\text{(by the sine subtraction formula)}\\ \nonumber
\sin\;(\theta - \phi) ~&=~ \tfrac{1}{\sqrt{13}}\\ \nonumber
&\Rightarrow\quad \theta - \phi ~=~ 0.281 \quad\text{or}\quad \theta - \phi ~=~ \pi - 0.281 = 2.861\\ \nonumber
&\Rightarrow\quad \theta ~=~ \phi \;+\; 0.281 \quad\text{or}\quad \theta ~=~ \phi \;+\; 2.861
\end{align*}\]
Now, since \(\;\cos\;\phi = \frac{2}{\sqrt{13}} \) and \(\phi \) is in QI, the most general solution for \(\phi \) is \(\phi = 0.983 + 2\pi k \) for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(... \). So since we needed to add multiples of \(2\pi \) to the solutions \(0.281 \) and \(2.861 \) anyway, the most general solution for \(\theta \) is:
\[\begin{align*}
\theta ~&=~ 0.983 \;+\; 0.281 \;+\; 2\pi k\quad\text{and}\quad 0.983 \;+\; 2.861 \;+\; 2\pi k\\
&\Rightarrow\quad \boxed{\theta ~=~ 1.264 \;+\; 2\pi k\quad\text{and}\quad 3.844 \;+\; 2\pi k}
\quad\text{for \(k=0 \), \(\pm\,1 \), \(\pm\,2 \), \(...\)}
\end{align*}\]
Note: In Example 6.8 if the equation had been \(\;2\,\sin\;\theta \;+\; 3\,\cos\;\theta ~=~ 1 \) then we still would have used a right triangle with legs of lengths \(2 \) and \(3 \), but we would have used the sine addition formula instead of the subtraction formula.
Find a General Solution to the Following Trigonometric Equation
Source: https://math.libretexts.org/Bookshelves/Precalculus/Book:_Elementary_Trigonometry_%28Corral%29/06:_Additional_Topics/6.01:_Solving_Trigonometric_Equations